konsep dasar besaran dan satuan

A. BESARAN DAN SATUAN

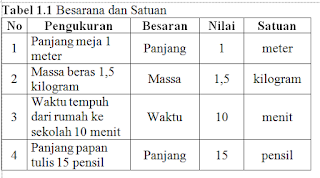
Besaran adalah sesuatu yang dapat diukur dan dapat dinyatakan dengan angka, sedangkan  pembanding dalam suatu pengukuran disebut satuan. Misalnya, anda melakukan kegiatan pengukuran panjang meja dengan pensil. Dalam kegiatan tersebut artinya anda membandingkan panjang meja dengan pensil. panjang pensil yang digunakan adalah sebagai satuan.

dari contoh diatas panjang, massa dan waktu disebut besaran, sedangkan untuk satuan meter, kilogram dan menit disebut satuan baku. untuk pensil disebut satuan tidak baku. satuan yang digunakan untuk melakukan pengukuran dengan hasil yang sama atau tetap untuk semua orang disebut satuan baku, sedangkan satuan yang digunakan untuk melakukan pengukuran dengan hasil yang tidak sama untuk orang yang berlainan disebut satuan tidak baku.

Besaran dalam fisika tebagi menjadi dua:

a. Besaran Pokok
besaran pokok yaitu besaran yang satuannya telah ditentukan secara internasional (SI) sebagai          dasar besaran lain (turunan).

    tujuh besaran pokok

b. Besaran Turunan

     besaran turunan, yaitu besaran yang satuannya diturunkan dari besaran pokok.

     beberapa besaran turunan, yaitu 

    besaran berdasarkan arahnya terdiri dari:

1. besaran skalar, besaran yang hanya meiliki nilai dan arah. contoh: massa (kg), kelajuan (m/s),            jarak (m) dan lain lain.

2. besaran vektor, besaran yang memiliki nilai dan arah. contoh: gaya, perpindahan, kecepatan,              percepatan, momentum.

B. DIMENSI BESARAN

     Dimensi besaran adalah cara suatu besaran tersusun atas besaran pokok

      contoh:tentuikan dimensi besaran gaya dan uasaha!

      gaya: F = m a

                F = Kg . m / s²

                F = [M].[L]/[T]2

                F = [M].[L][T]^{-2
         Usaha W = F s}

                W = Kg m / s². m

                W = M.LT^-2.L

                W = M.L² T^-2

Dimensi Besaran digunakan untuk :

a. membuktikan kesetaraan dua besaran

contoh:

Buktikan bahwa besaran momentum dan impuls adalah besaran yang setara!

P = m v                           

p = kg. m/s                  

P = [M]. [L] [T]^-1         

I = F.t

I = kg m/s² . s

I = [M] [L] [T]^-2. [T]¹

I = [M] [L] [T]^-2+1

I = [M] [L] [T]^-1    

b. membuktikan kebenaran suatu persamaan atau rumus

contoh:

buktikan bahwa rumus s = v . t bernilai benar! s = v. t

s = v. t

m = m s^-1. s¹

[L] = [L] [T]^-1 [T]¹

[L] = [L] [T]^-1+1

[L] = [L] [T]⁰

[L] = [L]

berarti rumus tersebut benar